8. Спички
Какое
минимальное количество спичек необходимо для того, чтобы выложить на плоскости n квадратов со стороной в одну спичку?
Спички нельзя ломать и класть друг на друга. Вершинами квадратов должны быть
точки, где сходятся концы спичек, а сторонами – сами спички.
Напишите
программу, которая по количеству квадратов n,
которое необходимо составить, находит минимальное необходимое для этого
количество спичек.
Вход. Одно
целое число n (1 ≤ n ≤ 109).
Выход. Вывести
минимальное количество спичек, требуемых для составления n квадратов.
|
Пример входа |
Пример выхода |
|
4 |
12 |
РЕШЕНИЕ
моделирование
Анализ алгоритма
Один
квадрат можно составить из 4 спичек. Два квадрата из 7 спичек. Очевидно, что
квадраты следует располагать так, чтобы они образовывали прямоугольник,
“близкий” к квадрату. Пусть width = ![]() – ширина этого
прямоугольника, length =
– ширина этого
прямоугольника, length = ![]() – длина. Для составления такого прямоугольника
понадобится width * (length + 1) + length * (width + 1)
спичек.
– длина. Для составления такого прямоугольника
понадобится width * (length + 1) + length * (width + 1)
спичек.
Останется
ost =
n – width * length квадратов, не поместившихся в этот прямоугольник. Их
пристроим отдельной строкой внизу прямоугольника, на что дополнительно
понадобится 2 * ost + 1 спичка.
Пример
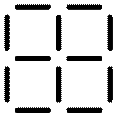
Покажем, как при помощи 12
спичек можно составить 4 квадрата.
Пусть
необходимо сложить n = 14 квадратов. Тогда
·
ширина прямоугольника width = ![]() = 3;
= 3;
·
длина прямоугольника length = ![]() = 4;
= 4;
Количество
спичек для укладки прямоугольника равно 3 * 5 + 4 * 4 = 31.
Число
оставшихся квадратов равно ost = 14 –
3 * 4 = 2, на которые потребуются 2 * 2 + 1 = 5 спичек.
Итого
потребуется 31 + 5 = 36 спичек, квадраты будут располагаться следующим образом.

Реализация алгоритма
Читаем
значение n. Вычисляем длину length и ширину width прямоугольника. Находим количество квадратов ost, которое не вошло в прямоугольник
размером length на width. Вычисляем требуемое количество
спичек.
scanf("%d",&n);
width = sqrt(1.0*n);
length = n / width; ost = n - width * length;
res = width * (length + 1) + length * (width +
1);
if (ost) res
= res + 2 * ost + 1;
Выводим ответ.
printf("%d\n",res);